BoundedResponse

Bounded Response

Bounded Response
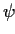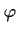INTENTION This pattern is applicable if one phenomenon, represented by $\psi$, always reacts on another phenomenon, represented by $\varphi$, with a maximal time delay $\tau$.
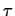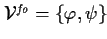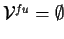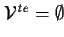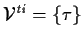SIGNATURE $\mathcal{V}^{\mathit{fo}} = \{\varphi, \psi\}$, $\mathcal{V}^{\mathit{fu}} = \emptyset$, $\mathcal{V}^{\mathit{te}} = \emptyset$, $\mathcal{V}^{\mathit{ti}} = \{\tau\}$
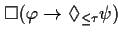FORMAL $\square( \varphi \rightarrow \lozenge_{\le \tau} \psi)$
NATURAL LANGUAGE Whenever 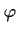$\varphi$ holds, then eventually within the next 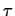$\tau$ time units, 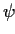$\psi$ is true.
Examples
EXAMPLE 1
  FORMAL $\square( [\mathit{malDetMach}] \rightarrow \lozenge_{\le 11} \mathit{userInformed})$
  NATURAL
LANGUAGE		 Whenever the machine starts assuming that there is a malfunction the user is informed about this within the next 11 time units.
Theorem Part
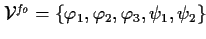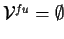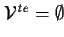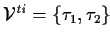THEOREM SIGNATURE $\mathcal{V}^{\mathit{fo}} = \{\varphi_1, \varphi_2, \varphi_3, \psi_1, \psi_2\}$, $\mathcal{V}^{\mathit{fu}} = \emptyset$, $\mathcal{V}^{\mathit{te}} = \emptyset$, $\mathcal{V}^{\mathit{ti}} = \{\tau_1, \tau_2\}$
THEOREM 1 Transitivity
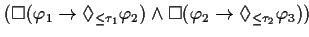
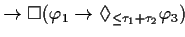  FORMAL $(\square( \varphi_1 \rightarrow \lozenge_{\le \tau_1} \varphi_2) \wedge \square( \varphi_2 \rightarrow \lozenge_{\le \tau_2} \varphi_3))$ $\rightarrow \square( \varphi_1 \rightarrow \lozenge_{\le \tau_1+\tau_2} \varphi_3)$
  EXPLANATION This theorem expresses the transitivity of this pattern.
THEOREM 2 Conclusion Distributivity over 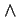$\wedge$
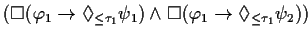
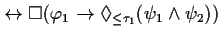  FORMAL $(\square( \varphi_1 \rightarrow \lozenge_{\le \tau_1} \psi_1) \wedge \square( \varphi_1 \rightarrow \lozenge_{\le \tau_1} \psi_2))$ $\leftrightarrow \square( \varphi_1 \rightarrow \lozenge_{\le \tau_1} (\psi_1 \wedge \psi_2))$
  EXPLANATION This theorem expresses the distributivity over 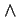$\wedge$ of the conclusions of two instantiations of this pattern.




 Übergeordnete Seite: Pp

 Feedback
Zu den Kontaktdetails des Verantwortlichen dieser Seite

 English
This page in english. Diese Seite auf englisch.