| Delayed Equivalence |
| INTENTION |
This pattern is applicable if one phenomenon, represented by the formula
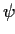 ,
is a time displaced copy of another phenomenon, represented by the
formula ,
is a time displaced copy of another phenomenon, represented by the
formula 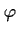 ,
with a maximal time delay ,
with a maximal time delay 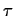 ,
i.e., ,
i.e., 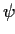 depends
always in the positive as well as in the negative case on
depends
always in the positive as well as in the negative case on
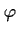 . . |
| SIGNATURE |
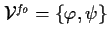 , ,
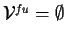 , ,
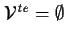 , ,
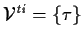 |
| FORMAL |
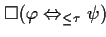 |
| NATURAL LANGUAGE |
Whenever 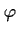 holds continuously for at least
holds continuously for at least 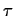 time units, then
eventually within this time span,
time units, then
eventually within this time span, 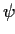 is true and remains true at
least as long as
is true and remains true at
least as long as 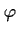 holds. And conversely, whenever
holds. And conversely, whenever 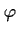 does
continuously not hold for at least
does
continuously not hold for at least 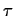 time units, then
eventually within this time span,
time units, then
eventually within this time span, 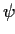 is false and remains false at
least as long as
is false and remains false at
least as long as 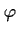 does not hold.
does not hold. |
| Examples |
| EXAMPLE 1 |
| |
FORMAL |
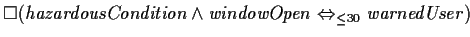 |
| |
NATURAL
LANGUAGE |
Whenever a window is continuously open during a hazardous condition for at
least 30 seconds, then eventually within this time span, a user is warned
and remains warned at least as long as this precondition is true. And
conversely, whenever a window is closed or there is no hazardous condition
for at least 30 time units, then eventually within this time span, the
user warning is suppressed and remains suppressed at least as long as this
precondition holds. |
| Theorem Part |
| THEOREM SIGNATURE |
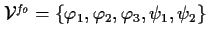 , ,
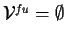 , ,
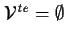 , ,
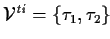 |
| THEOREM 1 Transitivity |
| |
FORMAL |
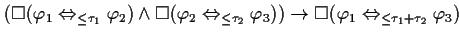 |
| |
EXPLANATION |
This theorem expresses the transitivity of this pattern. |
THEOREM 2 Conclusion
Distributivity over 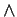 (One Direction)
(One Direction) |
| |
FORMAL |
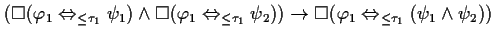 |
| |
EXPLANATION |
This theorem expresses the distributivity over 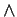 of the conclusions of two
instantiations of this pattern in one direction. Note that the other
direction is not a valid formula.
of the conclusions of two
instantiations of this pattern in one direction. Note that the other
direction is not a valid formula. |
![[Logo der AG Vernetzte Systeme]](/images/vs.gif)
