| Bounded Response |
| INTENTION |
This pattern is applicable if one phenomenon, represented by 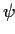 ,
always
reacts on another phenomenon, represented by ,
always
reacts on another phenomenon, represented by 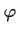 ,
with a maximal time
delay ,
with a maximal time
delay 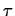 . . |
| SIGNATURE |
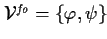 , ,
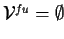 , ,
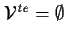 , ,
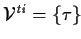 |
| FORMAL |
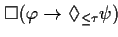 |
| NATURAL LANGUAGE |
Whenever 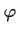 holds, then eventually within the next
holds, then eventually within the next 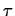 time
units,
time
units, 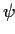 is true.
is true. |
| Examples |
| EXAMPLE 1 |
| |
FORMAL |
![$\square( [\mathit{malDetMach}] \rightarrow \lozenge_{\le 11}
\mathit{userInformed})$](img9.gif) |
| |
NATURAL
LANGUAGE |
Whenever the machine starts assuming that there is a malfunction the user
is informed about this within the next 11 time units. |
| Theorem Part |
| THEOREM SIGNATURE |
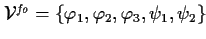 , ,
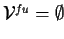 , ,
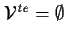 , ,
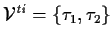 |
| THEOREM 1 Transitivity |
| |
FORMAL |
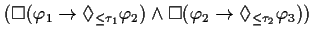
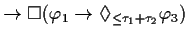 |
| |
EXPLANATION |
This theorem expresses the transitivity of this pattern. |
THEOREM 2 Conclusion
Distributivity over 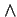 |
| |
FORMAL |
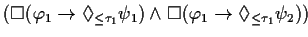
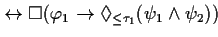 |
| |
EXPLANATION |
This theorem expresses the distributivity over 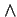 of the conclusions of two
instantiations of this pattern.
of the conclusions of two
instantiations of this pattern. |
![[logo of the networked systems group]](/en/images/vs.gif)
