| Limited Invariance |
| INTENTION |
This pattern is applicable if the fluttering of a phenomenon is
suppressed, i.e., if a phenomenon, represented by 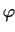 ,
reaches a
specific state, it remains in this state for at least ,
reaches a
specific state, it remains in this state for at least 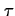 time
units.
time
units. |
| SIGNATURE |
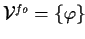 , ,
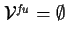 , ,
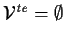 , ,
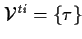 |
| FORMAL |
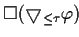 |
| NATURAL LANGUAGE |
Whenever 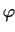 becomes true, it remains true for at least
becomes true, it remains true for at least 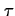 time
units.
time
units. |
| Examples |
| EXAMPLE 1 |
| |
FORMAL |
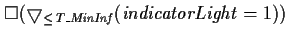 |
| |
NATURAL
LANGUAGE |
Whenever an indicator light is switched on, it remains for at least
T_MinInf time units. |
| Theorem Part |
| THEOREM SIGNATURE |
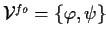 , ,
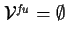 , ,
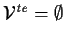 , ,
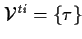 |
THEOREM 1 Expansion of
 over
over 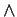 |
| |
FORMAL |
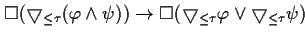 |
| |
EXPLANATION |
This theorem expresses how a conjunctive combination of two phenomena can
be expanded. |
THEOREM 2 Contraction of
 over
over 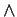 |
| |
FORMAL |
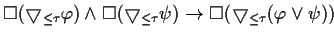 |
| |
EXPLANATION |
This theorem expresses how a conjunctive combination of two instantiations
of this pattern can be contracted. |
![[logo of the networked systems group]](/en/images/vs.gif)
